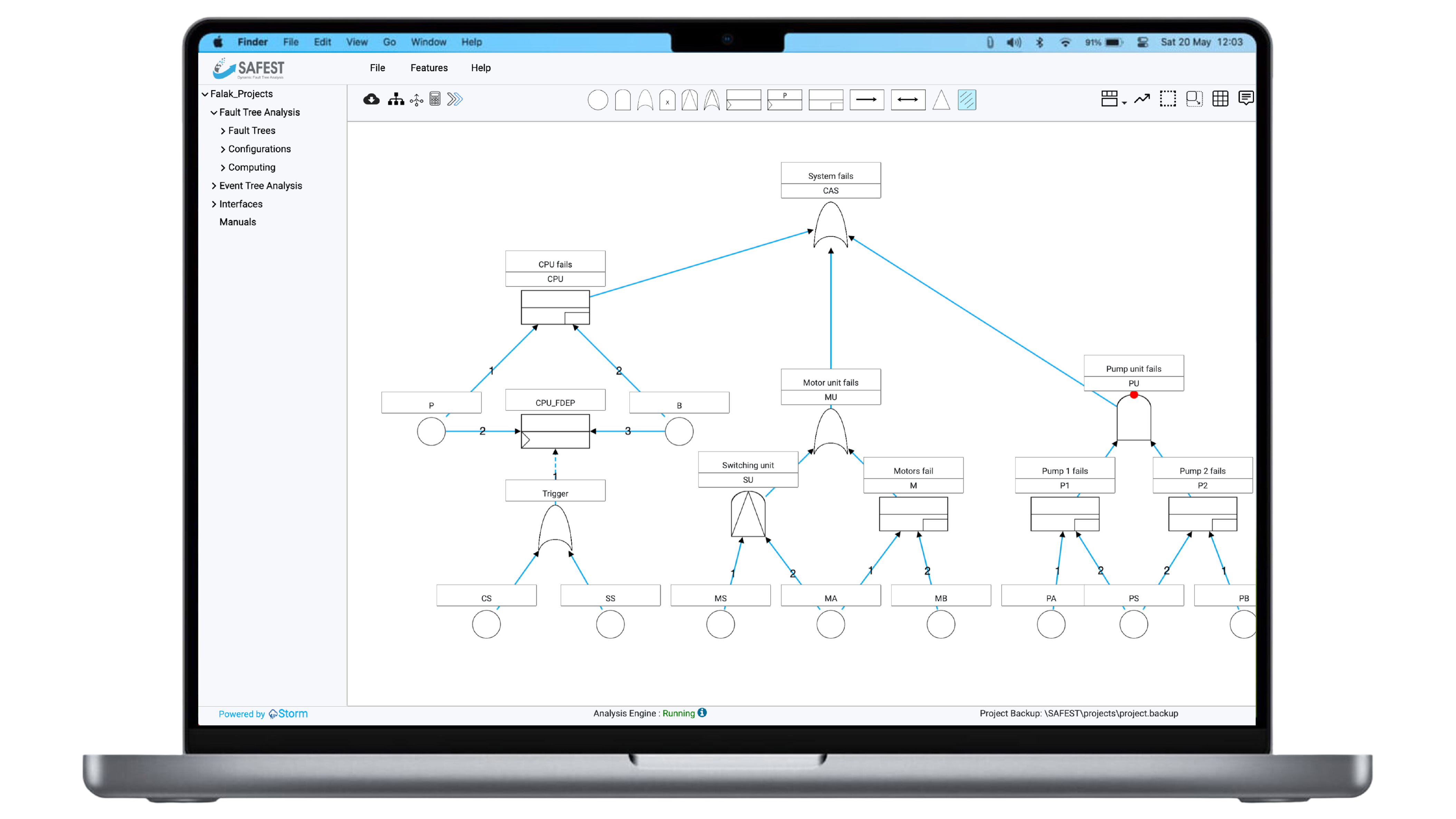
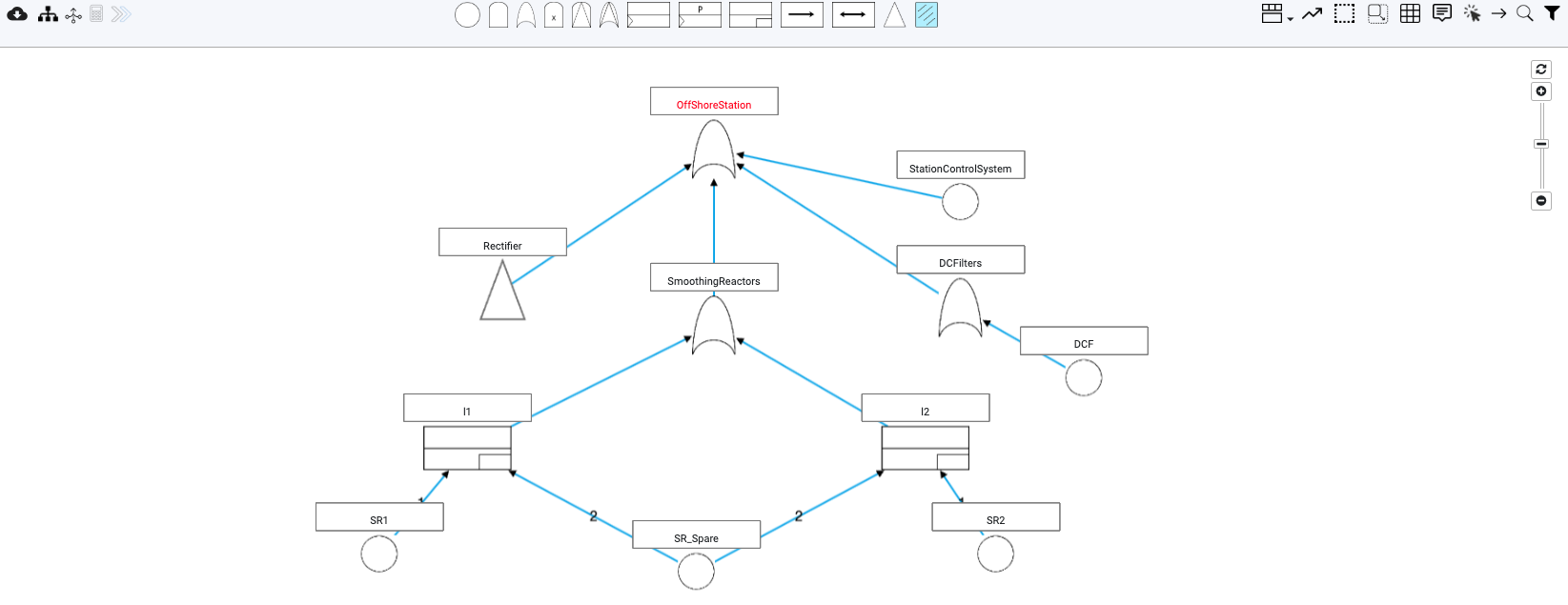
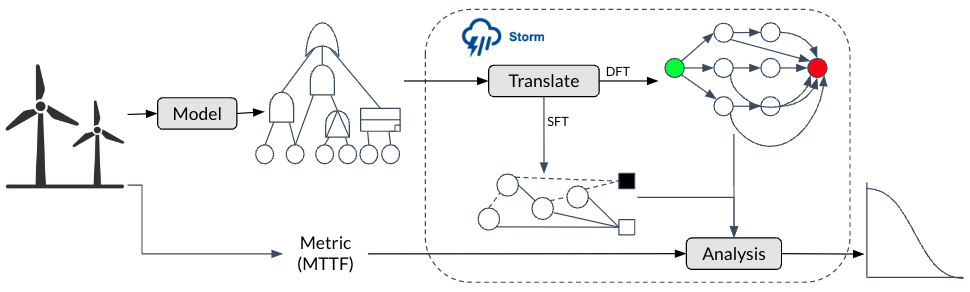
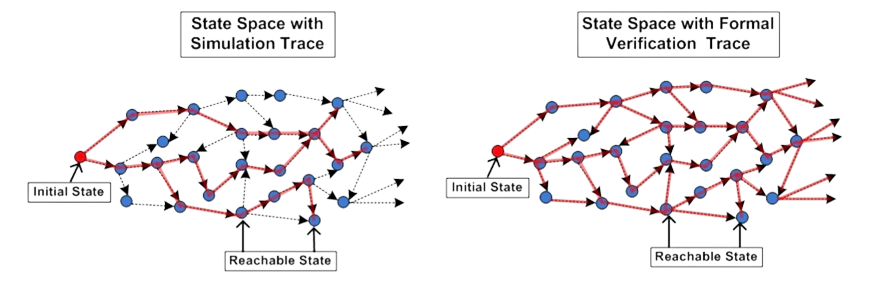
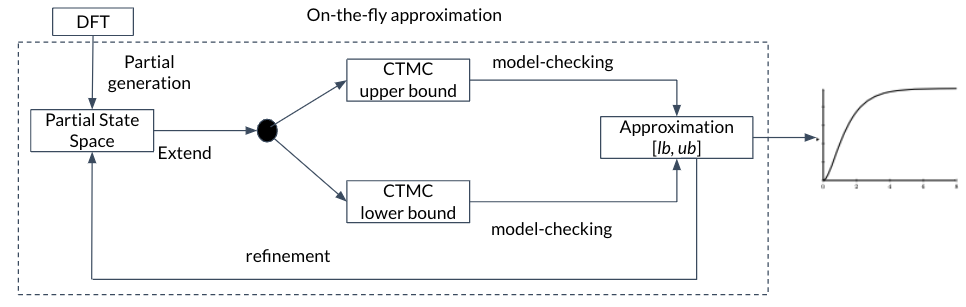
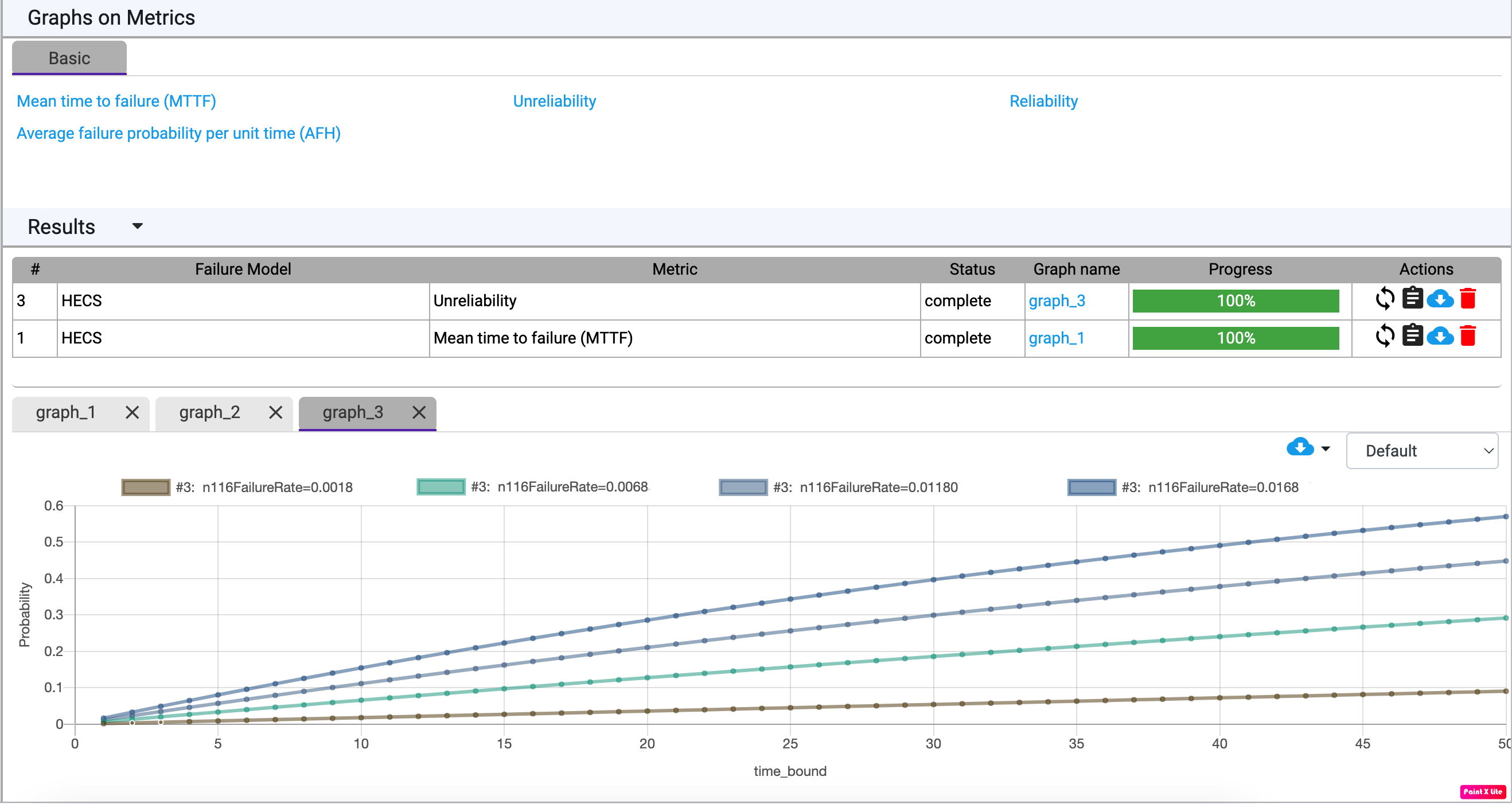
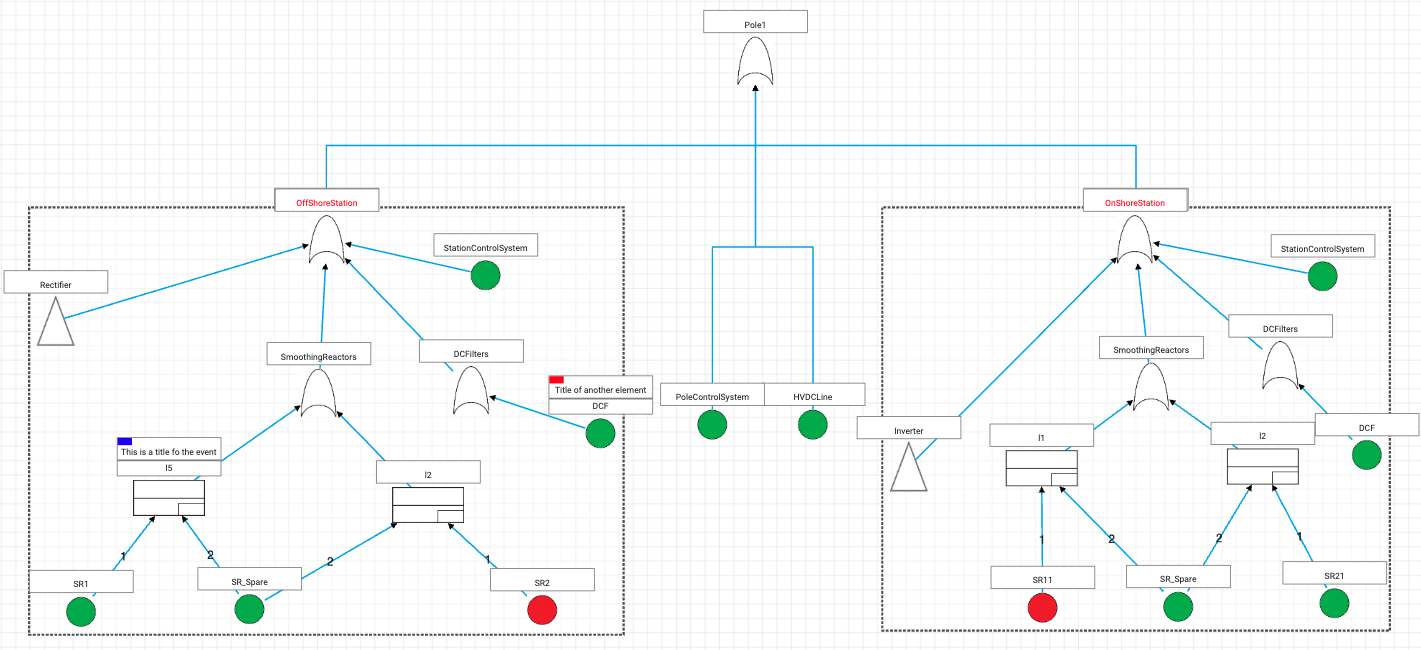
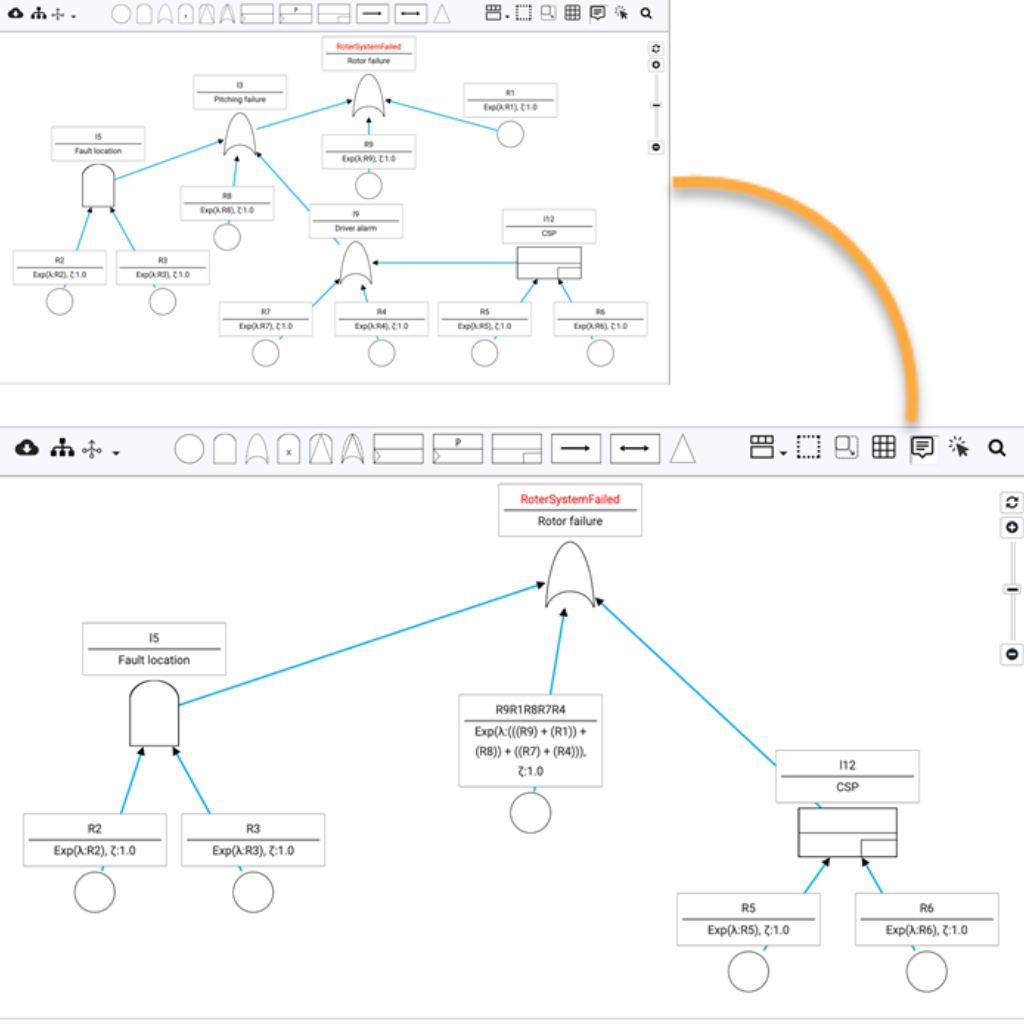
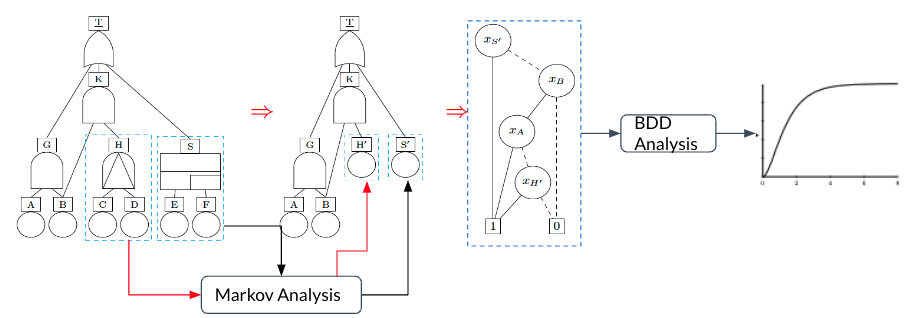
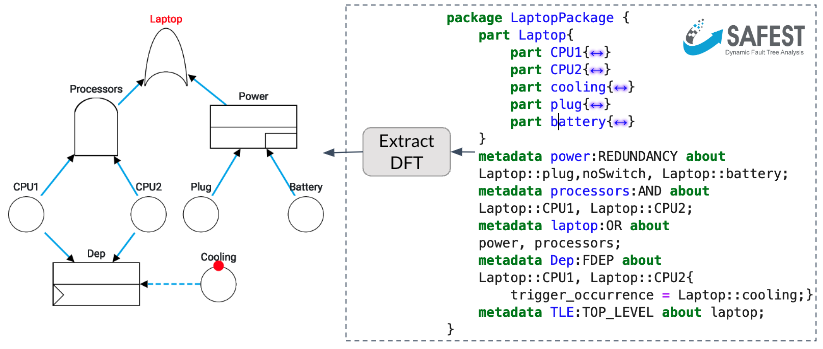
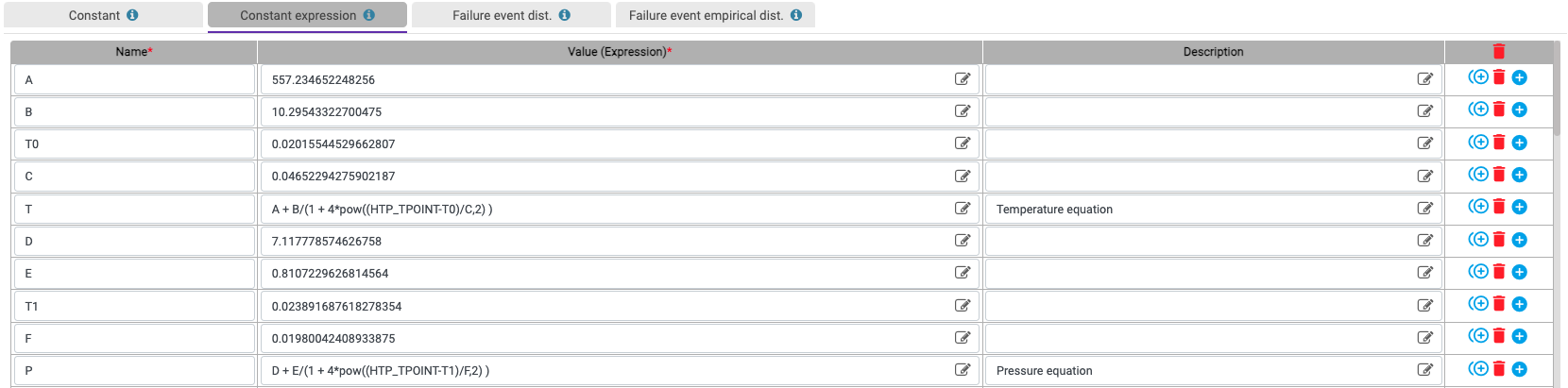
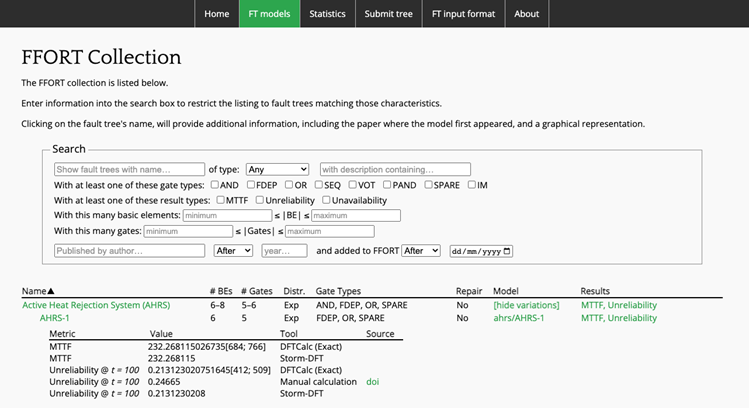
In order to accurately model large systems with redundancies, (probabilistic) functional dependencies, and temporal ordering among malfunctioning components—such as power plants, railroads, drones, medical equipment, satellites, and self-driving cars—static fault trees are too simplistic a formalism.
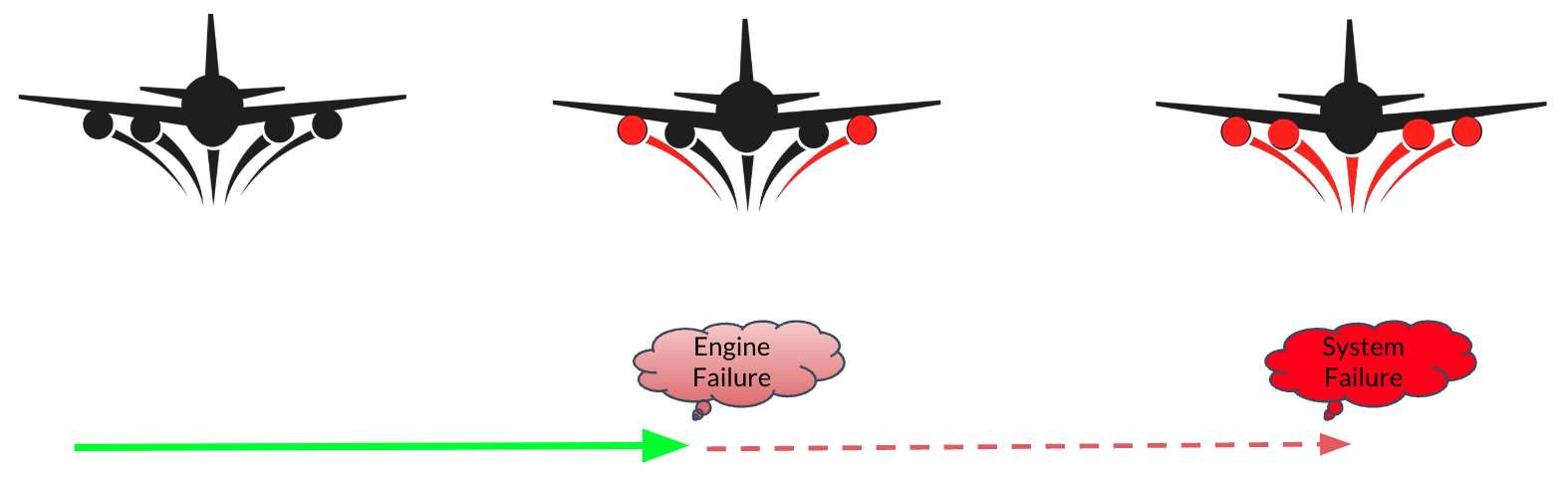
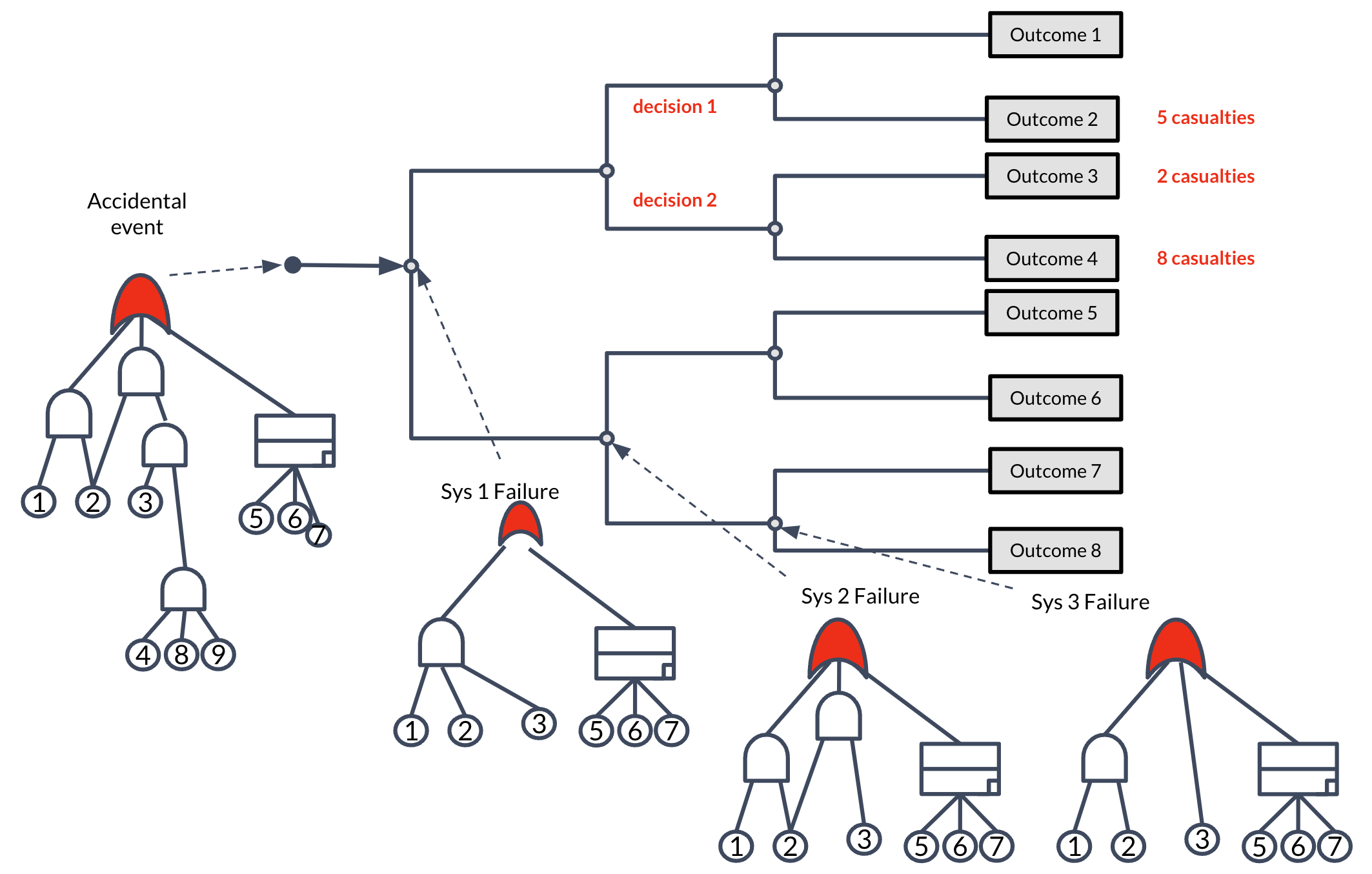
Similarly, event trees are unable to quantify losses such as the number of injuries, monetary loss, etc., or represent, for example, operators’ judgments following an accident, which may be necessary to lessen the impact of severe repercussions.
Dynamic fault trees and event trees overcome the above-mentioned shortcomings and, thus, enable the modeling and analysis of fail-operational/fault-tolerant dynamic systems.